Las matemáticas del amigo secreto

Pensemos un momento en el juego del amigo secreto de forma no convencional. ¿Se han sacado a sí mismos cuando toman el papelito? ¿Han visto que alguien en el mismo grupo de ustedes se saque a sí mismo? Y si ha sido así, ¿se han preguntado qué tan probable es que esas cosas hayan pasado?

Ya sé que no es muy común hacerse ese tipo de preguntas, pero calcular estas probabilidades es un ejercicio interesante que además tiene resultados más o menos curiosos. Acá comparto una aproximación a lo que sería una respuesta a esas preguntas.

¿Cómo podemos modelar un juego de amigo secreto? Hay varios opciones posibles, pero se me ocurre que la más sencilla es pensar en la repartición de los papelitos como una permutación. En efecto, supongamos que inicialmente cada persona anota su nombre en un papelito, después se colocan todos en una bolsa y cada uno escoge un papel de la bolsa. Existe entonces una función biyectiva entre los papelitos y la cantidad de personas. El concepto de permutación surge de forma natural. Digamos entonces que un juego de amigo secreto es simplemente una permutación $\sigma \in S_n$ , donde $n$ es la cantidad de personas que están jugando y $S_n$ es el grupo simétrico de orden $n$ .

Sin embargo, no es suficiente este concepto. Un juego de amigo secreto solo tiene sentido si cada persona escoge un papel distinto al suyo. En términos matemáticos, si $j$ es el papel que escribió una persona cualquiera entonces $\sigma(j)$ es el papel que saca de la bolsa. La condición de no sacarse a sí mismo se escribe como $j \neq \sigma(j)$ . En matemáticas esto quiere decir que el elemento $j$ no es un punto fijo de $\sigma$ . Pero ningún jugador se puede sacar a sí mismo, por lo que debe cumplirse que $\sigma(j) \neq j$ para todo $j=1,2,\cdots, n$ . Esta clase particular de permutaciones recibe el nombre de desarreglos.

Con estas consideraciones es fácil responder a la pregunta de qué tan probable es que en un juego con $n$ personas nadie se saque a sí mismo. Si asumimos que cada papelito se saca de forma aleatoria con distribución uniforme, entonces dicha probabilidad está dada por

$\mathbb{P} \big(\text{Nadie se saque a si mismo} \big) = \dfrac{\text{Cantidad de desarreglos}}{\text{Cantidad de permutaciones posibles}}$

Sea $|D_n| = \text{Cantidad de desarreglos}$ y $|S_n| =\text{Cantidad de permutaciones posibles}$ . Calcular $|S_n|$ es elemental: si pensamos que una permutación de $S_n$ es una función entre $n$ cajitas y $n$ peloticas distinguibles y que cada pelotica debe ir en una caja, entonces para la primera caja hay un total de $n$ posibles peloticas, para la segunda, dado que ya se colocó alguna en la primera caja, solo hay $n-1$ peloticas posibles y así sucesivamente. Por tanto, se llega a la muy conocidísima relación

$|S_n| = n(n-1)(n-2) \cdots 1 = n!$

Calcular $|D_n|$ es considerablemente más retador. Para ello podemos usar el siguiente razonamiento recursivo, clásico en teoría combinatorial, pero también con pelotas y cajas. Supongamos que se coloca una pelota en la caja $1$ . Como buscamos desarreglos, solo hay $n-1$ posibilidades para la pelota que se puso en esa caja. Llamemos a esa pelota $j$ . Ahora bien, los casos restantes se pueden dividir en dos conjuntos disjuntos de posibilidades: si en la caja $j$ se coloca la pelota $1$ , entonces el problema es equivalente a olvidarnos de esas cajas y buscar el número de desarreglos en $S_{n-2}$ , es decir, buscar $|D_{n-2}|$ . Si por el contrario la pelota $1$ no se coloca en la caja $j$ , entonces debemos hallar los desarreglos de $S_{n-1}$ . Poniendo todo esto junto y usando las reglas combinatoriales del producto y de la suma, tenemos que

$|D_n| = (n-1) \big( |D_{n-1}| + |D_{n-2}|)$

Consideramos que $|D_0| = 1$ por vacuidad y que $|D_1| = 0$ . Esto es claro, pues en una permutación de un solo elemento no pueden existir desarreglos. Ahora bien, hallar una fórmula cerrada para $|D_n|$ no es algo particularmente elemental, ya que en general la solución de las ecuaciones en diferencias no es simple. La prueba la dejaré al final de esta entrada usando funciones generadoras, por si alguien está interesado. El punto importante es que una fórmula cerrada para $|D_n|$ está dada por

$|D_n| = n! \displaystyle \sum_{\ell = 0}^n \dfrac{(-1) ^{ \ell}}{\ell!}$

Así pues, la probabilidad que buscamos desde el principio está dada por

$\mathbb{P} \big(\text{Nadie se saque a si mismo} \big) = \dfrac{n! \displaystyle \sum_{\ell = 0}^n \dfrac{(-1) ^{ \ell}}{\ell!}}{n!} = \displaystyle \sum_{\ell = 0}^n \dfrac{(-1) ^{ \ell}}{\ell!}$

Pero aquí es donde comienzan las cosas sorprendentes. ¿Qué les dice la intuición acerca de la relación entre la probabilidad de que nadie se saque a sí mismo y el número de personas que juegan? ¿Qué pasa si jugamos un amigo secreto con un millón de personas? ¿Esa probabilidad es alta, es baja?

Observemos que si $n \rightarrow \infty$ nuestra probabilidad tiende a

$\displaystyle \sum_{\ell = 0}^{\infty} \dfrac{(-1) ^{ \ell}}{\ell!}$

¡Y esta serie converge! Y de hecho converge a algo conocido. Es la serie de potencias de la función exponencial evaluada en $-1$ , por lo que de hecho tenemos

$\displaystyle \sum_{\ell = 0}^{\infty} \dfrac{(-1) ^{ \ell}}{\ell!} = \dfrac{1}{e} \approx 0.36788$

Esto quiere decir entonces que la probabilidad de que en un juego de amigo secreto con $n$ personas al menos alguien se saque a sí mismo está dada por

$\mathbb{P} \big(\text{Al menos una persona se saque a si misma} \big) = 1- \displaystyle \sum_{\ell = 0}^{n} \dfrac{(-1) ^{ \ell}}{\ell!}$

Pero lo impresionante es, insisto, en que de hecho esta probabilidad converge. Para quedar sorprendido piénselo así: si jugamos un amigo secreto con todos los habitantes de la tierra, con una probabilidad del $63.2$ % al menos alguien se va a sacar a sí mismo. Y esa probabilidad es casi la misma que si juega solo con $20$ personas. Y además esto quiere decir que en aproximadamente el $60$ % de los amigos secretos que usted ha jugado en la vida, alguien se ha sacado a sí mismo y se ha tenido que repetir la repartición. ¿Bastante impresionante, no?

Como las cosas se entienden más fácil con simulaciones, hagamos un pequeño experimento para ver todas estas matemáticas en acción. Tomando $n \in \lbrace 2, 3, \cdots, 100 \rbrace$ , y para cada uno de estos valores, hice $10000$ simulaciones de juegos de amigos secreto (esto es, escoger permutaciones de $n$ ) y para cada uno de esos juegos determiné si el juego es válido o no (es decir, si la permutación es un desarreglo o no) y sumé esa cantidad de juegos inválidos. Si todo lo que hicimos es correcto, para cada $n$ nuestra observación es una realización de $X_n \sim \text{Bin}(n, p)$ donde

$p = \displaystyle \sum_{\ell = 0}^n \dfrac{(-1)^{\ell}}{\ell !}$

y por lo tanto la razón teórica dada por la variable aleatoria binomial mencionada arriba y la razón observada entre los juegos fallidos y los juegos totales deben ser similares.

En ese sentido el siguiente gráfico parece darnos la razón:

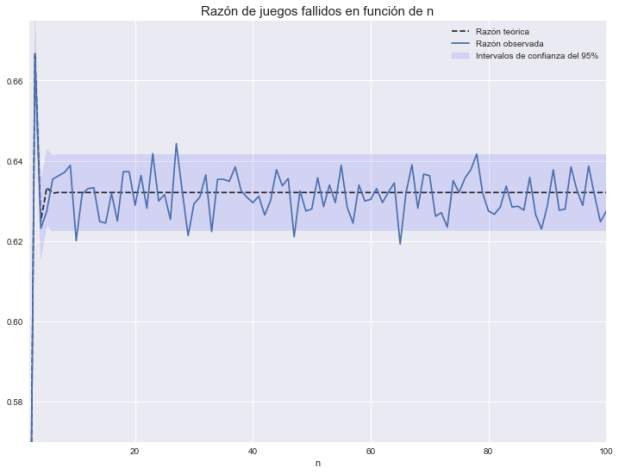
Confianza

Tal vez sea mucho más simple usar una de esas aplicaciones en donde nadie se saca a sí mismo, ¿no?

Cálculo de la fórmula cerrada para $|D_n|$ .

Dada nuestra fórmula de recurrencia para $|D_n|$ , podemos usar funciones generadoras para hallar su valor cerrado. En particular, usaremos la función generadora exponencial dada por

$F(x) = \displaystyle \sum_{n = 0}^{\infty} |D_n| \dfrac{x^n}{n!}$

Dado que nuestra ecuación de recurrencia es equivalente a $|D_{n+1}| = n(|D_n| + |D_{n-1}|)$ tenemos

$\displaystyle \sum_{n = 0}^{\infty} n|D_{n+1}| \dfrac{x^n}{n!} = \displaystyle \sum_{n = 0}^{\infty} n|D_n| \dfrac{x^n}{n!} + \displaystyle \sum_{n = 0}^{\infty} n |D_{n-1}| \dfrac{x^n}{n!}$

Por otro lado, tenemos que

$F'(x) = \displaystyle \sum_{n = 1}^{\infty} |D_n| \dfrac{x^{n-1}}{(n-1)!} =\displaystyle \sum_{n =0}^{\infty} |D_{n+1}| \dfrac{x^{n}}{n!}$

Además,

$xF'(x) = \displaystyle \sum_{n = 1}^{\infty} |D_n| \dfrac{x^n}{(n-1)!} = \displaystyle \sum_{n = 1}^{\infty} n|D_n| \dfrac{x^n}{n!} = \displaystyle \sum_{n = 0}^{\infty} n|D_n| \dfrac{x^n}{n!}$

Ahora calculemos $xF(x)$ :

$xF(x) = \displaystyle \sum_{n = 0}^{\infty} |D_n| \dfrac{x^{n+1}}{n!} = \displaystyle \sum_{n = 0}^{\infty} (n+1)|D_n| \dfrac{x^{n+1}}{(n+1)!} = \displaystyle \sum_{n = 1}^{\infty} n |D_{n-1}| \dfrac{x^{n}}{n!} = \displaystyle \sum_{n = 0}^{\infty} n |D_{n-1}| \dfrac{x^{n}}{n!}$

Por lo tanto, tenemos que

$F'(x) = xF'(x) + F(x)$

Y esto es equivalente a $\dfrac{F'(x)}{F(x)} = \dfrac{1}{1-x} - 1$ . Cuando se resuelve esta ecuación diferencial con la condición inicial $F(0) = 0$ se obtiene

$F(x) = \dfrac{e^{-x}}{1-x}$

Usando las series de taylor para las funciones $e^{-x}$ y $\dfrac{1}{1-x}$ tenemos

$F(x) = \Bigg( \displaystyle \sum_{n=0}^{\infty} \dfrac{(-1)^n x^n}{n!} \Bigg) \cdot \Bigg( \displaystyle \sum_{k=0}^{\infty}(-1)^k x^k \Bigg)$

Y finalmente, por la fórmula del producto de Cauchy, podemos escribir

$F(x) = \displaystyle\sum_{n=0}^{\infty} \Bigg( \displaystyle\sum_{\ell=0}^{n} \dfrac{(-1) ^{2n-\ell}}{(n-\ell) !} \Bigg) x^n = \displaystyle\sum_{n=0}^{\infty} \Bigg( \displaystyle\sum_{\ell=0}^{n} \dfrac{(-1) ^{\ell}}{(n-\ell) !} \Bigg) x^n = \displaystyle\sum_{n=0}^{\infty} \Bigg( \displaystyle\sum_{\ell=0}^{n} \dfrac{n! (-1) ^{\ell}}{\ell !} \Bigg) \dfrac{x^n}{n!}$

Y los coeficientes de esta serie son precisamente $|D_n|$ , por lo que tenemos el resultado.

Las matemáticas del amigo secreto

Cálculo de la fórmula cerrada para $|D_n|$ .

Publicado por Carlos Andrés Osorio Alcalde

1 comentario

Deja un comentario Cancelar la respuesta

Cálculo de la fórmula cerrada para .

Comparte:

Publicado por Carlos Andrés Osorio Alcalde

1 comentario

Deja un comentario Cancelar la respuesta

Cálculo de la fórmula cerrada para $|D_n|$ .